
Luxembourg Science Center
La médiatrice scientifique Gina Reuland lors d'une show sur la statistique au Luxembourg Science Center.
56 %, 95 % ou étaient-ce plutôt 99 % ? Les médias comparent et résument souvent les taux d’efficacité des différents vaccins en évoquant de simples pourcentages. Mais qu'est-ce que ces valeurs reflètent exactement ? Quelle est leur précision ? Et qu'est-ce que cela signifie lorsque les chercheurs mentionnent des intervalles entiers dans leurs études ? Dans le présent article, nous examinerons ces questions de plus près et essayerons de déchiffrer les concepts statistiques qui s'y rapportent.
Afin de mieux comprendre les concepts statistiques des études, nous simulons une étude qui fait la lumière sur le stéréotype selon lequel les femmes luxembourgeoises sont plus douées pour faire du multitâche que les hommes. Un échantillon de cent femmes et de cent hommes participe à l'étude. Pendant un intervalle de temps déterminé, les participants sont invités à accomplir deux tâches en même temps, par exemple, rédiger un message et écouter une conversation. Ensuite, l’équipe de chercheurs vérifie si ces tâches ont été effectuées correctement et indique le nombre de femmes et d’hommes qui y sont parvenus.
Si 60 % des femmes de l’échantillon ont réussi les deux tâches, une extrapolation à la population totale avec l’affirmation « 60 % des femmes au Luxembourg sont capables de faire du multitâche » s’avèrerait peu sérieuse d’un point de vue statistique. Pourquoi ? Il se pourrait que l’échantillon n’ait pas été bien choisi, malgré les efforts pour le déterminer avec le plus grand soin possible. Dans quelle mesure pouvons-nous donc avoir confiance dans les résultats d'une telle étude ?
Un échantillon bien choisi, une conception adéquate de l’étude et une analyse statistique des données sont des facteurs importants pour obtenir des résultats fiables et pertinents.
Qu’est-ce qu’un bon échantillon ?
Un échantillon a été bien choisi s’il est représentatif de la population, c’est-à-dire s’il reflète le mieux possible l'ensemble de la population avec toutes ses caractéristiques. « Avec toutes ses caractéristiques », ce n’est pas un concept très concret, c’est pourquoi la représentativité en soi n’est pas une expression scientifique.
La signification est toutefois largement reconnue et claire : l’échantillon doit représenter le mieux possible la population. Les chercheurs identifient les caractéristiques de la population qui sont pertinentes pour leur étude et tirent au hasard des sujets dans chaque couche de la population présentant la caractéristique identifiée. Ces caractéristiques doivent être représentées dans l'échantillon en fonction de leur proportion réelle dans la population.
Idéalement, on utilise également un tel échantillon aléatoire stratifié pour les études sur l’efficacité des vaccins ou des médicaments devant être autorisés pour l'ensemble de la population. Dans ce cas, les principales caractéristiques seraient, par exemple, le sexe, l'âge, l'indice de masse corporelle et l'origine.
Dans la pratique, cependant, ce n'est pas toujours le cas. Ainsi, les personnes âgées, par exemple, sont souvent exclues des essais cliniques. Une des raisons en est qu’elles souffrent souvent de plusieurs maladies en même temps, ce qui rend plus difficile la tâche de déterminer l’efficacité d’un médicament et/ou d’identifier pourquoi des effets secondaires peuvent survenir.

Au Luxembourg Science Center, on peut estimer à l’aide d’un échantillon (on tire 25 boules parmi 1 000) combien de boules rouges se trouvent dans la grande sphère. Dans l’échantillon sur la photo, quatre des 25 boules sont rouges (voir l’écran en arrière-plan), ce qui équivaudrait à environ 160 boules rouges au total.
Dans quelle mesure les études représentatives sont-elles fiables ?
Même si on a choisi un bon échantillon représentatif, la règle suivante s’applique : si le résultat d’une étude s’appuie uniquement sur un seul échantillon, il est très rare qu’il corresponde exactement à la valeur réelle recherchée de l’ensemble de la population. Pour cela, il faudrait que l'ensemble de la population participe à l'étude. Il y aura toujours des écarts.
C’est pourquoi les intervalles que les chercheurs signalent souvent avec leurs résultats dans les études sont essentiels. Ces intervalles, également appelés intervalles de confiance, indiquent une fourchette qui comprend très probablement la valeur réelle de la population cherchée. En d'autres termes, un intervalle de confiance de 95 % peut être décrit comme suit : si les chercheurs répétaient l’étude à cent reprises, 95 des 100 intervalles indiqués contiendraient la valeur réelle de la population totale et pour cinq intervalles, ce ne serait pas le cas. Ainsi, dans 95 cas sur 100, le résultat de l’étude serait fiable.
Infobox
Sur la base de leur échantillon aléatoire, les chercheurs déterminent une fourchette qui contient très probablement la valeur réelle recherchée de la population. Voici comment ils procèdent :
Avant de réaliser leur étude, les chercheurs déterminent la probabilité qu’ils se trompent et que la valeur réelle ne se situe pas dans l'intervalle calculé. Cette marge d’erreur est souvent de l’ordre de 5 %.
Pourquoi 95 % et non pas 100 % ? Plus on s’approche des 100 %, plus l’intervalle s’agrandit et plus il est difficile de détecter des différences statistiquement significatives entre deux groupes – mais nous y reviendrons. Ainsi, un taux de certitude de 95 % s'est avéré utile et a été accepté dans de nombreux domaines de recherche.
Qu’est-ce que cela signifie pour la pertinence de notre étude fictive décrite ci-dessus ? Les chercheurs calculeraient deux intervalles de confiance, un pour les hommes et un pour les femmes, qui estiment la position respective de la valeur réelle de la population. Si les intervalles se chevauchent à la fin, aucune différence statistiquement significative dans la capacité de faire du multitâche ne peut être constatée entre les hommes et les femmes. En revanche, si elles ne se chevauchent pas, il existe une différence statistiquement significative entre les sexes ! Et nous pouvons avoir confiance dans ce résultat.
Tu peux le simuler toi-même dans le graphique interactif suivant. Déplace le curseur pour modifier la proportion des femmes (pF) et des hommes (pM) capables de faire du multitâche observé dans l'échantillon et examine quand les intervalles de confiance (zones jaune et bleue sous les courbes) se chevauchent et quand ce n’est pas le cas. Tu peux aussi modifier la taille des échantillons (n) d'hommes et de femmes. Tu constateras, par exemple, qu’avec un échantillon composé de cent femmes respectivement de cent hommes et une capacité de faire du multitâche des femmes de 60 % (pF = 0,6), la différence entre les deux groupes en ce qui concerne la capacité de faire du multitâche serait statistiquement significative si elle était d’au moins 20 points de pourcentage, c’est-à-dire si pM ≤ 0,4 ou pM ≥ 0,8.
Que se passe-t-il lorsque la taille de l’échantillon augmente ?
Les intervalles de confiance se réduisent à mesure que la taille de l’échantillon augmente, ce qui rend notre estimation plus précise et augmente la pertinence de l’étude ! Si les chercheurs souhaitent réduire de moitié l’intervalle de 95 %, donc pour ainsi dire doubler la précision de l’étude, ils doivent multiplier par quatre la taille de l'échantillon. Ainsi, en déterminant la taille de l’échantillon, les scientifiques définissent la largeur de l’intervalle de confiance et, partant, la pertinence de leur étude.
Et si les chercheurs souhaitaient tester la capacité de faire du multitâche non pas des Luxembourgeois, mais des Allemands, des Américains, des Chinois ou de l'ensemble de la population mondiale ? Dans ce cas, la taille de l'échantillon devrait-elle augmenter proportionnellement à la taille de la population ?
Pas forcément ! La méthode de l’échantillon aléatoire stratifié garantit en principe que l’échantillon sélectionné représente une petite population de façon aussi fiable que ce serait le cas avec une plus grande population. Mais plus la taille de l’échantillon est grande, plus l’intervalle de confiance sera petit et plus l’étude sera précise et pertinente.
Qu’est-ce que cela signifie dans le contexte des études sur les vaccins contre la Covid-19 ?
En janvier 2021, des demandes d’autorisation pour l'utilisation d'urgence de vaccins ont été déposées dans l’UE pour les vaccins contre la Covid-19 d’AstraZeneca, de Moderna et de BioNTech/Pfizer. En mars, le vaccin de Johnson & Johnson a suivi. L’Agence européenne des médicaments (EMA) a accordé des autorisations de mise sur le marché pour le vaccin Vaxzevria d’AstraZeneca sur la base des résultats intermédiaires d'essais cliniques. Examinons ces résultats de plus près.
Au total, 5 807 sujets ont reçu le vaccin et 5 829 se sont vu administrer un placebo. Dans le premier groupe, 30 personnes ont développé une forme symptomatique de la Covid-19, et dans le second groupe, elles étaient 101. Dans ce contexte, l’efficacité d’un vaccin correspond au pourcentage de sujets qui ont été épargnés par la maladie grâce au vaccin. Qu’est-ce que cela signifie concrètement ?
Étant donné que dans le groupe vacciné, 101-30 = 71 sujets de moins sont tombés malades que dans le groupe témoin, ce sont précisément ces sujets qui ont été en moyenne épargnés par la maladie, ce qui correspond à une efficacité d'environ 70% dans l'étude publiée. Cela signifie qu’en moyenne, près de 70 personnes vaccinées sur 100 qui entrent en contact avec le virus sont protégées contre la maladie. En d’autres termes, si toute la population du Luxembourg avait été vaccinée avec le vaccin d’AstraZeneca avant la pandémie, il n’y aurait probablement pas eu 70 000 cas d’infection, mais seulement 21 000 sur la base des données actuelles (début juin 2021).
Bien entendu, nous avons désormais besoin d’un intervalle de confiance pour évaluer la fiabilité de ce taux d’efficacité de 70,4 % qui s’est dégagé des essais cliniques. Un facteur important pour déterminer la largeur de l’intervalle est le rapport entre la proportion de malades de la Covid-19 dans le groupe vacciné et celle dans le groupe témoin - c'est ce que l’on appelle le risque relatif.
Dans l’étude d’AstraZeneca, 30 des 5 807 sujets du groupe vacciné sont tombés malades, soit 0,52 %. Dans le groupe témoin, ce pourcentage était de 1,73 %. Le risque relatif est donc de 0,52/1,73 = 0,3. Moins il y a de personnes malades dans le groupe vacciné et plus il y a de personnes malades dans le groupe témoin, plus ce rapport diminue. Un risque relatif plus faible augmente notre confiance dans l’efficacité du vaccin et s’accompagne donc d’un intervalle de confiance plus petit et plus précis et d'une étude plus pertinente.
Le tableau suivant indique la taille de l’échantillon, le risque relatif, l’efficacité et l’intervalle de confiance des essais sur les vaccins des quatre grands groupes pharmaceutiques.
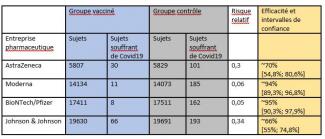
Concrètement, pour l’exemple du vaccin d’AstraZeneca, cela signifie que : le taux d’efficacité du vaccin dans l’échantillon de l’étude clinique était d’environ 70 %. Mais dans l’ensemble de la population, il devrait toutefois se situer entre 55 et 81 % environ. À noter que les taux d’efficacité signalés dans le tableau se réfèrent seulement à la réduction du nombre de malades infectés et non pas à la sévérité des maladies ou aux cas de décès, la vaccination ayant bien entendu un impact positif à cet égard. Ici, dans les études sur le vaccin de Johnson & Johnson, on a constaté une protection de 85 %, et pour les vaccins d’AstraZeneca, de BioNTech/Pfizer et de Moderna, elle était chaque fois de 100 % !
Conclusion
Les méthodes statistiques nous permettent donc, à l’aide d’échantillons, de tirer des conclusions sans trop de difficultés sur la population totale. Bien entendu, la représentativité de l’échantillon est déterminante dans ce contexte, sans quoi tout résultat perd de sa pertinence. Ainsi, les meilleures statistiques ne peuvent montrer que ce que les échantillons permettent de révéler. Toutefois, si ces concepts sont utilisés consciencieusement et sur la base de données fiables, il est possible de tirer des conclusions précises pour l’ensemble de la population.
Auteurs: Gina Reuland & Julien Meyer (Luxembourg Science Center)
Éditeur: Michèle Weber (FNR)
Photo: Luxembourg Science Center
Simulation: Gina Reuland & Julien Meyer à l'aide de GeoGebra







