Puissance et limites des maths face aux flambées épidémiques

Suite aux développements inquiétants concernant la dynamique du virus Covid-19, le gouvernement luxembourgeois a annoncé récemment des mesures plutôt restrictives afin de limiter la propagation de l’épidémie.

Incontestablement subtile de trouver le bon équilibre entre le respect des libertés individuelles, fortement ancré dans notre compréhension démocratique, la protection de l’économie et le contrôle de la propagation du virus, le bon choix des mesures tend vers le dilemme. Ainsi, une connaissance étroite et précise de la situation est incontournable. La Covid-19 Taskforce de Research Luxembourg a (entre autres) comme objectif d’analyser et d’évaluer régulièrement la situation et de rapporter au gouvernement afin de soutenir les prises de décisions.

D’un point de vue mathématique, cette analyse se fait par le biais de modèles qui font l’écart entre la situation actuelle, telle qu’elle se présente réellement, et le futur. Modéliser c’est se projeter dans un futur plus ou moins proche tout en sachant qu’on navigue dans des mondes possibles qui dépendent étroitement des hypothèses nécessairement simplificatrices qu’on utilise pour refléter la réalité. Tout l’art revient donc à synthétiser en équations ce qui compte vraiment, en faisant abstraction du reste. D’où l’importance de données fiables comme point de départ.

La croissance exponentielle, l’alter ego des virus

Dans sa note d’information du 23 octobre, la Taskforce précisait indubitablement que la situation est urgente : la dynamique de propagation du virus avait montré, au cours des 7 jours précédents un effet exponentiel croissant. Même si cette dynamique s’est ralentie un peu au cours de la semaine passée, elle montre toujours un effet exponentiel. Buzzword ces derniers mois, beaucoup d’entre nous ont sûrement développé une intuition basique de cette croissance accélérée et du fait que, pour éviter une propagation chaotique du virus, son éviction est clé. Mais pourquoi ? Qu’est-ce que la quintessence d’une telle croissance et qu’est-ce qui la rend aussi inquiétante ? Et peut-être le plus important : comment l’arrêter ?

Françoise Kemp, mathématicienne au Luxembourg Centre for Systems Biomedicine (LCSB) et membre de la Taskforce, explique : « Les virus sont des exemples classiques de croissance exponentielle car, in fine, ce qui cause de nouveaux cas, ce sont les cas existants ! ». La croissance exponentielle d’une série de nombres se caractérise en effet par la simple règle qu’on passe d’un nombre au suivant en multipliant par un facteur fixe, par exemple 2. On pense à l’échiquier du sage Sissa, qui, selon la légende, demandait comme récompense à son roi, un échiquier rempli de riz : « Sur la première case, posez 1 grain de riz, sur la deuxième case, posez 2, sur la troisième case 4 et ainsi de suite. » De manière générale, pour aller d’une case à l’autre, on multiplie le nombre de grains chaque fois par 2. On dit que la quantité de riz croît de manière exponentielle. En faisant la somme, les comptables du roi se rendaient vite compte que la récompense demandée par Sissa n’était pas aussi modeste qu’initialement prévu : le nombre de grains de riz est en effet supérieur au nombre total d’insectes estimé vivre sur terre !

Echiquier de Sissa (Wikimedia Commons)

Quid des virus ? Afin de mieux comprendre leur caractère exponentiel, imaginons un cas de figure dans lequel chaque personne infectée I soit en contact étroit avec en moyenne 4 personnes chaque jour.  Supposons de plus que chaque contact provoque une nouvelle infection dans un quart des cas, encore en moyenne. En écrivant finalement  ΔI le nombre des nouveaux infectés, nous trouvons l’équation

Le fait que I détermine sa propre variation accélère incontestablement les choses : si I est grand, sa variation l’est également. Autrement dit, beaucoup d’infectés entraînent beaucoup de nouvelles infections. En appelant I1 respectivement I2 le nombre d’infectés au jour 1 et 2, nous voyons que

De manière générale, nous multiplions par 2 le nombre d’infectés en passant d’un jour à l’autre, et retrouvons une croissance exponentielle identique à celle des grains de riz. Sur deux mois, à savoir 61 jours (comparable aux 64 cases de l’échiquier) ceci fait un tas d’infectés…

Mettons ces observations en musique en passant aux données fournies par la Taskforce : Ci-dessous la figure 2 de sa note d’information du 30 octobre 2020 qui indique le nombre d’infectés total dans le temps. Nous avons rajouté deux sliders qui permettent de jouer sur les paramètres suivants :

• le nombre moyen de contacts sociaux par personne (orange)
• la probabilité qu’un tel contacte aboutisse à une infection (bleu)

En supposant un début de croissance exponentielle à partir de début octobre, essayez de reproduire au mieux la situation telle qu’elle se manifeste actuellement. En extrapolant la courbe, cela fournit des projections similaires à la courbe représentée en vert pointillé sur la figure calculée par la Taskforce. Un simple calcul permet alors de déterminer le temps de doublement T, c’est-à-dire le temps après lequel le nombre d’infectés double.

Parvenez-vous à retrouver le temps de doublement estimé par la Taskforce, à savoir à peu près 6 jours ?

Simulation superposée sur la figure 2 du rapport de la Task Force du 30 octobre. Dans le graphique de la Task Force, les nombres officiels de cas de COVID-19 jusqu'au 29 octobre (points rouges) ont été approximés avec un modèle adapté pour les prévisions à court terme. L'évolution au cours des 4 dernières semaines indique un comportement exponentiel (zone verte). Un ajustement linéaire forcé (orange) ne peut pas bien décrire les données. Cela est lié à une dynamique épidémique exponentielle très volatile qui ne peut être atténuée que par des efforts sociaux communs. Pour simuler ces efforts, bougez les sliders « nombre de contacts/personne » (orange) et probabilité d’une infection (bleu) pour voir l’impact sur la courbe verte superposée sur le graphique de la Task Force.

L’approche mathématique qu’illustre l’extrapolation de la courbe exponentielle nous permet donc de quantifier la situation actuelle afin de faire des prévisions qui aident à la prise et justification de certaines décisions. N’oublions néanmoins pas que l’hypothèse sous-jacente que « rien ne change » ne permet que d’évaluer la situation à court terme : Y aura-t-il de nouvelles mesures ?  Comment ces mesures seront-elles adoptées par la population ? Quel sera l’effet des retours des vacances, de l’ouverture des écoles ? De plus, l’hypothèse intrinsèque à l’exponentielle, qui interdit toute forme de prévisions à moyen et long terme, est que la population dans laquelle propage le virus est infinie. Si l’exponentielle peut croître sans limites en théorie, la réalité est fort différente. En effet, sans hypothèses supplémentaires, et en se restreignant sur le Luxembourg comptant à peu près 600'000 habitants, avec un temps de doublement de 6 jours et 1000 personnes infectées au départ, toute la population du Luxembourg serait infectée au bout d’à peu près 54 jours, une situation totalement irréaliste et non fondée.

Le modèle SIR

Pour ses projections à moyen terme, la Taskforce utilise des modèles dits compartimentaux. Ces modèles tiennent cette fois-ci bien compte de la taille de la population et la divisent en plusieurs classes épidémiologiques. Un modèle assez simple mais particulièrement intéressant est le modèle SIR. Les lettres S, I et R représentent les 3 compartiments de ce modèle, à savoir les personnes Saines (ou Susceptibles), les personnes Infectées et finalement les personnes guéries (ou « Recovered » en anglais). Notons que les compartiments peuvent être plus fins (et c’est bien le cas des modèles de la Taskforce), en ajoutant des catégories pour par exemple les décédés, les nouveau-nés, les personnes en quarantaine etc. Le but est alors de spécifier des règles selon lesquelles évolue l’épidémie, c’est-à-dire les conditions sous lesquelles une personne peut passer d’une catégorie à une autre.

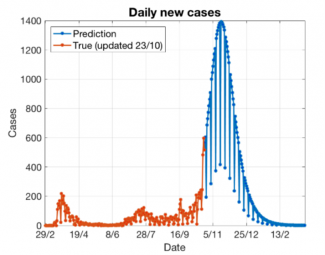
Figure 4 de la note d’information de la Taskforce du 2 novembre. La courbe bleue a été calculé par un modèle se basant sur le SIR.

Intéressons-nous d’abord aux infectés. Similairement à ce que nous venons de voir pour la croissance exponentielle, la variation des infectés, que nous notons I ' ci-dessous, se compose des personnes saines qui s’infectent moins les personnes infectées qui guérissent. De manière schématique le modèle se dessine comme suit :

Le nombre de personnes saines qui s’infectent se détermine comme auparavant par le nombre de contacts n par unité de temps et la probabilité p d’une infection transmise lors d’un contact. De plus, appelons γ le taux de guérison. Ceci permet d’ajouter aux flèches des labels qui correspondent au nombre de personnes qui passe d’une catégorie à l’autre :

De manière équivalente, le schéma se réécrit sous forme de 3 équations aux inconnues S, I et R comme

S' = — np⋅SI
I' = np⋅SI — γI
R' = γI

Afin de déterminer la dynamique de l’épidémie dans le temps, il suffit de résoudre ces équations dites « d’évolution ». En principe, il faudrait des cours de mathématiques avancées afin de résoudre et comprendre toutes les subtilités de ces équations ; or il existe aujourd’hui des logiciels simples et accessibles à tout le monde qui peuvent faire le travail pour nous.

Le logiciel ci-dessous nous permet de simuler la dynamique d’une épidémie en partant avec 1% d’infectés sur toute la population. Ce point de départ, essentiel dans toutes les projections, est en réalité difficile à estimer et revient à contrôler au mieux le nombre de personnes infectés non recensés. D’où l’intérêt des tests à grande échelle et de l’analyse des eaux usées. Les courbes jaune, rouge et verte représentent l’évolution des susceptibles, infectés et guéris. En bougeant les sliders, vous pouvez expérimenter avec les paramètres définissant le modèle et observer leurs effets sur par exemple l’évolution des personnes infectés. Notons aussi que le nombre de contacts et la probabilité d’infection lors d’un contact sont exactement les paramètres que nous, en tant que citoyens, peuvent influencer.  En effet, des gestes barrières comme le port du masque vont baisser la probabilité d’infection lors d’un contact. Similairement, des mesures restrictives telles que celles votées par le parlement le 29 octobre (maximum 4 personnes sans gestes barrières et couvre-feu pendant la nuit) vont baisser le nombre de contacts. Le taux de guérison peut surtout être influencé par de meilleurs traitements et médicaments.

Notez qu’avec les paramètres comme ils sont prédéfinis, la courbe des infectés (rouge) représente un pic qui correspond à une situation dans laquelle à peu près la moitié de la population s’infecterait dans un intervalle de temps assez réduit. Une telle situation déclencherait incontournablement une grave crise du système de santé, une situation qu’il faut éviter. En jouant sur les paramètres, n’oubliez donc surtout pas le verset de prière épidémiologique : Flatten the curve !

Simulation de la population susceptible de contracter une infection COVID-19 (S, courbe jaune), de la fraction des infectés (I, courbe rouge) et des personnes guéries (R, courbe verte) en fonction du temps. En bougeant les sliders p, n et y, on peut changer la probabilité d'infection lors d'un contact, le nombre de contacts et le taux de guérison et voir quel impact ces différentes variables peuvent avoir sur les courbes S, I et R.

Que pouvons-nous conclure de tout ceci ? Déjà que les modèles mathématiques nous permettent de quantifier certains développements et d’en tirer des conclusions. Ceci peut faciliter la prise de décision et justifier certaines mesures, tout en sachant que personne, et aucun modèle, ne pourra appréhender et intégrer toutes les conséquences sociales, économiques et psychologiques qui en découlent. Néanmoins, l’aperçu d’un futur (au pire) possible que les mathématiques nous offrent nous permet d’agir et de réagir de manière fondée et adaptée ce qui n’est déjà pas mal.

Auteur: Julien Meyer (Luxembourg Science Center)

Éditeurs: Christophe Ley (professeur de statistique mathématique au Département de mathématiques appliquées, informatique et statistique de l'Université de Gand), Michèle Weber (FNR)

Illustrations : Wikimedia Commons, Research Luxembourg, Julien Meyer

Simulations : Julien Meyer (en utilisant geogebra.org et en se basant sur des données/graphiques du rapport de Research Luxembourg)