https://commons.wikimedia.org/wiki/File:Casino_dices.jpg
„Just one time!“ Wer kennt ihn nicht, diesen flehenden Schrei verzweifelter Pokerspieler*innen, die in einer Hand weit hinten liegen und kurz vor dem Ausscheiden stehen? Sie beten zu den Göttern für einen Glücksfall, um nur dieses eine Mal wieder ins Spiel zu finden. Aber abgesehen von diesen seltenen Momenten des Ruhmes verfluchen die Spieler*innen solche zufälligen Schwankungen, die nur allzu leicht eine unvorhersehbare Wendung in kurzer Zeit herbeiführen, ob im Casino oder an der Börse. Aber diese Glücksritter*innen sind nicht die Einzigen, die sich vor Schwankungen fürchten!
Man denke nur an Forscher*innen, die auf ihrer Suche nach Wissen Rückschläge erleiden und vor durch die Launen des Zufalls verursachten Dilemmata stehen. Wunderheilungen, überraschende Wahlergebnisse und unvorhersehbare Wetterwechsel! Wenn die Allgegenwart von Zufallsschwankungen die Gültigkeit aller Hypothesen in Frage stellt, wie können wir dann in diesem erratischen Hintergrundrauschen das Relevante erkennen?
Die Werkzeuge und Methoden der Statistik sind in der heutigen wissenschaftlichen Forschung allgegenwärtig und ermöglichen die Analyse und Auswertung großer Datenmengen in so unterschiedlichen Bereichen wie Soziologie, Medizin oder Experimentalphysik. Dennoch erfordert ihre Anwendung eine ehrliche und experimentelle Herangehensweise, um voreilige oder fehlerhafte Interpretationen und Schlussfolgerungen zu vermeiden.
Eine Hypothese überprüfen: gar nicht so einfach!
Auf der Suche nach Wissen entwerfen Forscher*innen routinemäßig Experimente, um ihre Hypothesen zu testen. Aber Vorsicht, der Erfolg eines schlecht gewählten Tests bestätigt nicht unbedingt die Gültigkeit der Hypothese! Nehmen wir das Bild des Hahns [1], der mit seinem schallenden Krähen jeden Morgen die Sonne hervorzulocken scheint. Genügt es nicht, ihn Tag für Tag triumphierend krähen zu sehen, um die Hypothese „Der Hahn lockt die Sonne durch sein Krähen hervor“ zu bestätigen?
Um zu versuchen, diese falschen Beweise zu eliminieren, entwickelte Ronald Fisher (1890-1962), der Chefstatistiker der British agricultural experiment station, in der ersten Hälfte des 20. Jahrhunderts das Konzept der Nullhypothese. Grundsätzlich genügt es, das Gegenteil von dem zu betrachten, was man zeigen möchte. Im vorherigen Beispiel hieße die Nullhypothese also „Der Hahn hat keinen Einfluss auf den Aufgang der Sonne“. Die wissenschaftliche Methode würde dann darin bestehen, zu versuchen, die Nullhypothese zu widerlegen, indem man zeigt, dass die Abwesenheit des Hahns die Nacht auf ewig verlängert. Aber natürlich geht die Sonne auch auf, wenn der Hahn in den Topf gewandert ist! Wir kommen daher zu dem Schluss, dass sich aus der Beobachtung kein Einfluss des Hahns auf den Sonnenaufgang nachweisen lässt.
[1] Siehe Tangente n°182 (mai-juin 2018) : Les mystères cachés des probas et des stats, p.36-37
Ronald Fisher 1913
Copyright: Wikipedia. Public Domain
Konkreter: Denken wir an die Prüfung der Wirksamkeit einer neuen Behandlung gegen eine Infektionskrankheit. Nach den Regeln der Kunst wird das betreffende Medikament einer Gruppe von Patient*innen verabreicht. Die Entwicklung dieser Patient*innen wird mit der einer weiteren Gruppe verglichen, die lediglich ein Placebo erhalten hat (Kontrollgruppe). Die Nullhypothese ist, dass das neue Medikament keine Wirkung hat. Wenn diese Hypothese in Anbetracht der gemachten Beobachtungen sehr unwahrscheinlich erscheint, wird die Nullhypothese verworfen und von der Wirksamkeit des Medikaments ausgegangen.
Wie lässt sich einschätzen was wahrscheinlich ist und was nicht?
Es besteht ein klarer Bedarf, ein strenges Maß einzuführen, das unsere Beobachtungen auf objektivere Weise quantifiziert. Dieses als p-Wert (für engl. probability value) bezeichnete Maß definieren Mathematiker als die Wahrscheinlichkeit, ein Ergebnis zu erhalten, das mindestens so „extrem“ ist wie das beobachtete, während die Nullhypothese erfüllt ist. Im Allgemeinen wird, wenn der p-Wert unter einem bestimmten Schwellenwert liegt, die Nullhypothese verworfen und das Ergebnis als statistisch signifikant angesehen.
Infobox
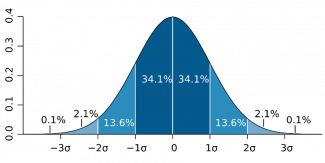
Je spektakulärer die Ankündigung einer Forschungsgruppe erscheint, desto mehr erwartet die wissenschaftliche Gemeinschaft natürlich handfeste Beweise. Als die Forscher*innen des CERN 2012 die Existenz des berühmten Brout-Englert-Higgs-Bosons bekanntgaben, sprachen sie beispielsweise von einer Wahrscheinlichkeit von 5 Sigma, was einem p-Wert von etwa 
entspricht. Mit anderen Worten: Unter der Annahme, dass das Boson nicht existiert, wären die erhaltenen Ergebnisse eine rein zufällige Schwankung, die im Durchschnitt in 3,5 Millionen identischen Experimenten einmal auftritt. Extrem unwahrscheinlich, aber dennoch nicht unmöglich! Die Wahrscheinlichkeit, bei „Kopf oder Zahl“ 22 Mal in Folge Kopf zu erhalten, ist übrigens genauso hoch.
Simulation des Zerfalls eines bei der Kollision von zwei ultrahochenergetischen Protonen entstandenen Higgs-Bosons. Die gelben Linien stellen die möglichen Wege der Partikel dar, die bei der Kollision entstanden sind, wogegen die abgelegte Energie dieser Partikel in blau dargestellt ist.
© 1997-2021 CERN (Lizenz: CC-BY-SA-4.0)
Infobox
geschrieben, Sigma gesprochen), die Schwankungen um den Mittelwert in einer Folge von identischen Zufallsexperimenten misst. Oft werden die Ergebnisse von Experimenten durch eine Glockenkurve, auch Gauß-Kurve genannt, modelliert. 1 Sigma gibt dann an, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Mittelwert liegen. In ähnlicher Weise gibt 2 Sigma an, dass etwa 95 % der Werte innerhalb von zwei Standardabweichungen vom Mittelwert liegen usw. In der Teilchenphysik wird ein 3-Sigma-Ergebnis als Beobachtung bezeichnet, während ein 5-Sigma-Ergebnis als Entdeckung gilt.
Die Bedeutung eines ehrlichen und experimentellen Vorgehens in der Statistik
Ist die Nullhypothese also ein Patentrezept, das es uns erlaubt, mechanisch das Relevante vom Hintergrundrauschen der Schwankungen zu unterscheiden? Sicherlich nicht! In seinen beiden Haupttexten, Statistical Methods for Research Workers (1925) und The Design of Experiments (1935), warnt Fisher selbst, dass der Statistiker, um relevante und signifikante Ergebnisse zu erhalten, zunächst seine Vorstellungskraft, seine Kreativität und vor allem sein tiefes Wissen über ähnliche Daten und Beobachtungen kombinieren muss, bevor er entscheidet, welche Hypothesen sich zur Überprüfung eignen. Die Wahl einer Nullhypothese, der kritischen Schwelle für den p-Wert und die Gestaltung des Experiments selbst sind eine Kunst, die sich nicht auf einen automatisierten Prozess reduzieren lässt. Die Wahrheit einer Aussage mit statistischen Methoden zu belegen, ist außerdem etwas, das nur durch eine Kombination von wiederholten Experimenten, vorzugsweise durch mehrere unabhängige Forschungsgruppen, erfolgen kann.
Ohne zusätzlichen Kontext und Vorwissen sind die diskutierten Methoden und Konzepte daher weder in der Lage, Wahres von Falschem zu unterscheiden, noch eine Kausalität zwischen verschiedenen Phänomenen eindeutig zu belegen. Wenn sie jedoch ehrlich und gewissenhaft angewandt werden, erlauben sie uns, fundierte Schlussfolgerungen zu ziehen, von denen wir mit gutem Grund glauben können, dass sie relevant sind.
Autor*innen: Julien Meyer, Gina Reuland (Luxembourg Science Center)
Editorin: Michèle Weber (FNR)
