Stärken und Grenzen der Mathematik angesichts von Krankheitsausbrüchen

Angesichts der beunruhigenden Entwicklungen hinsichtlich der Dynamik des COVID-19-Virus kündigte die luxemburgische Regierung vor kurzem eher restriktive Maßnahmen an, um die Ausbreitung der Epidemie zu begrenzen.

Es ist zweifelsohne schwierig, ein gutes Gleichgewicht zwischen der Achtung der in unserem Demokratieverständnis fest verankerten persönlichen Freiheiten, dem Schutz der Wirtschaft und der Kontrolle der Verbreitung des Virus zu finden. Die Verantwortlichen stehen bei der Wahl der richtigen Maßnahmen vor einem Dilemma. Aus diesem Grund ist ein tiefgehendes und genaues Verständnis der Lage von äußerster Wichtigkeit. Ziel der COVID-19 Task Force von Research Luxembourg ist es (unter anderem), die Situation regelmäßig zu analysieren und zu evaluieren und Bericht an die Regierung zu erstatten und damit die Entscheidungsfindung zu unterstützen.

Aus mathematischer Sicht erfolgt diese Analyse über Modelle, welche die Abweichung zwischen dem Ist-Zustand, wie er sich aktuell darstellt, und der Zukunft berechnen. Modellieren bedeutet, sich in eine mehr oder weniger ferne Zukunft zu versetzen, wohlwissend, dass man sich hier in möglichen Welten bewegt, die sehr stark von notwendigerweise vereinfachenden Hypothesen abhängen, mit denen die Realität abgebildet werden soll. Die Kunst besteht also darin, das, was wirklich zählt, in Gleichungen zusammenzufassen, während alles andere außer Acht gelassen wird. Das ist auch der Grund, aus dem verlässliche Daten als Ausgangspunkt so wichtig sind.

Exponentielles Wachstum, das Alter Ego des Virus

In ihrem Bericht vom 23. Oktober weist die Task Force unmissverständlich darauf hin, dass die Lage alarmierend ist: Die Ausbreitung des Virus hatte in den sieben Tagen vorher ein exponentielles Wachstum aufgewiesen. Auch wenn sich die Entwicklung in der letzten Woche ein wenig verlangsamt hat, verläuft das Wachstum nach wie vor exponentiell. „Exponentielles Wachstum“ war das Schlagwort der letzten Monate. Viele von uns haben ein grundlegendes Gespür dafür entwickelt, dass es sich dabei um ein beschleunigtes Wachstum handelt, das unbedingt aufgehalten werden muss, um eine chaotische Ausbreitung des Virus zu vermeiden. Aber warum? Worin besteht das Wesen eines solchen Wachstums, und was macht es so besorgniserregend? Und, die vielleicht wichtigste Frage: Wie lässt es sich aufhalten?

Françoise Kemp, Mathematikerin am Luxembourg Centre for Systems Biomedicine (LCSB) und Mitglied der Task Force, erklärt: „Viren sind klassische Beispiele für exponentielles Wachstum, denn letztlich sind es bestehende Fälle, die neue Fälle verursachen!“ Das exponentielle Wachstum einer Zahlenreihe zeichnet sich durch die einfache Regel aus, dass man die nächste Zahl erhält, indem man die vorherige mit einem festen Faktor, zum Beispiel 2, multipliziert. Man denke an das Schachbrett des Weisen Sissa, der sich einer Legende zufolge von seinem König als Belohnung ein Schachbrett mit Weizenkörnern erbat: „Legt auf das erste Feld ein Weizenkorn, auf das zweite Feld zwei, auf das dritte Feld vier und immer so weiter.“ Von einem Feld zum nächsten verdoppelte sich also die Zahl der Weizenkörner. Man kann auch sagen, die Menge der Weizenkörner wuchs exponentiell an. Bei der Berechnung merkten die Rechenmeister des Königs recht schnell, dass die von Sissa geforderte Belohnung gar nicht so bescheiden war, wie zunächst gedacht: Die Zahl der Weizenkörner übersteigt tatsächlich die geschätzte Zahl der auf der Erde lebenden Insekten!

Schachbrett des Sissa (Wikimedia Commons)

Was bedeutet das für Viren? Um den exponentiellen Charakter besser zu verstehen, gehen wir davon aus, dass jede infizierte Person  jeden Tag im Schnitt mit vier Personen engen Kontakt hat. Weiterhin nehmen wir an, dass diese Kontakte im Schnitt in einem Viertel der Fälle zu einer Neuinfektion führen. Wenn wir die Zahl der Neuinfizierten mit  benennen, erhalten wir die Gleichung

Die Tatsache, dass  seine eigene Variation bestimmt, beschleunigt das Ganze zweifelsohne: Wenn  groß ist, ist seine Variation es auch. Anders gesagt: Viele Infizierte führen zu vielen Neuinfektionen. Wenn  und  die Zahl der Infizierten an Tag 1 und 2 bezeichnen, sehen wir, dass

Die Zahl der Infizierten verdoppelt sich also von einem Tag auf den nächsten, und wir haben es hier mit einem exponentiellen Wachstum zu tun, das dem der Weizenkörner entspricht. In zwei Monaten, das heißt 61 Tagen (vergleichbar mit den 64 Feldern des Schachbretts), haben wir da schon einen Haufen Infizierte ...

Setzen wir diese Beobachtungen anhand der Daten der Task Force in die Praxis um: Hier sehen Sie die Abbildung 2 ihres Berichts vom 2. November, welche die Zahl der Infizierten gesamt im zeitlichen Verlauf darstellt. Wir haben zwei Schieber hinzugefügt, mit denen sich die folgenden Parameter verändern lassen:

• die durchschnittliche Anzahl an sozialen Kontakten pro Person
• die Wahrscheinlichkeit, dass ein solcher Kontakt zu einer Infektion führt

Gehen Sie von einem Beginn des exponentiellen Wachstums Anfang Oktober aus und versuchen Sie, die Situation, wie sie sich gegenwärtig darstellt, bestmöglich abzubilden. Extrapoliert man die Kurve, ergeben sich ähnliche Voraussagen wie die aus der von der Task Force berechneten grün gestrichelten Kurve in der Abbildung. Die Verdopplungszeit T, das heißt die Zeit, nach der sich die Zahl der Infizierten verdoppelt hat, lässt sich dann ganz einfach berechnen.

Gelingt es Ihnen, die von der Task Force zugrunde gelegte Verdopplungszeit von fast sechs Tagen zu finden?

Simulation über Abbildung 2 des Berichts von Research Luxembourg vom 30. Oktober. Die Näherung der offiziellen COVID-19-Fallzahlen bis zum 29. Oktober (rote Punkte) erfolgte mit einem an kurzfristige Vorhersagen angepassten Modell. Die Entwicklung der letzten vier Wochen zeigt, dass ein exponentielles Wachstum (grüner Bereich) und eine festgelegte lineare Anpassung (orange) als Erklärung für die Daten nicht ausreichend sind. Das hat mit einer stark schwankenden exponentiellen Dynamik der Epidemie zu tun, die sich nur durch gemeinsame soziale Anstrengungen abschwächen lässt. Um diese Veränderungen zu simulieren, bewegen Sie die Schieber „Anzahl der Kontakte/Person“ (orange) und „Wahrscheinlichkeit einer Infektion“ (blau) und betrachten Sie die Auswirkungen auf die Veränderung der grünen Kurve, die wir über die Grafik der Task Force gelegt haben.

Der mithilfe der Extrapolation der exponentiellen Kurve illustrierte mathematische Ansatz ermöglicht es uns also, die aktuelle Lage zu beziffern, um Voraussagen treffen zu können, die als Begründung für bestimmte Entscheidungen dienen. Es darf allerdings nicht vergessen werden, dass die zugrundeliegende Annahme, dass sich „nichts verändert“, dazu führt, dass nur die kurzfristige Situation analysiert werden kann: Wird es neue Maßnahmen geben?  Wie werden diese Maßnahmen von der Bevölkerung angenommen? Welche Auswirkungen werden Urlaubsrückkehrer und die Öffnung der Schulen haben?  Darüber hinaus liegt dem exponentiellen Wachstum die Hypothese zugrunde, dass die Population, in der sich das Virus verbreitet, unendlich ist, was jede Art von mittel- und langfristigen Vorhersagen unmöglich macht. Auch wenn sich das exponentielle Wachstum in der Theorie unendlich fortsetzen kann, sieht die Realität doch ganz anders aus. Wenn man von weiteren Hypothesen absieht und sich auf Luxemburg mit seinen etwa 600.000 Einwohnern beschränkt, wäre bei einer Verdopplungszeit von sechs Tagen und 1.000 Infizierten als Ausgangspunkt nach etwa 54 Tagen die gesamte luxemburgische Bevölkerung infiziert – ein vollkommen unrealistisches Szenario, das jeder Grundlage entbehrt.

Das SIR-Modell

Für ihre mittelfristigen Vorhersagen nutzt die Task Force sogenannte Kompartimentmodelle. Diese Modelle berücksichtigen die Größe der Population und teilen sie in verschiedene epidemiologische Klassen ein. Ein recht einfaches, aber besonders interessantes Modell ist das SIR-Modell. Die Buchstaben ,  und  stehen für die drei Gruppen der Gesunden (Susceptibles), Infizierten und Genesenen (Recovered). Die Kompartimente können auch noch kleinteiliger sein (was auch bei den Modellen der Task Force der Fall ist), indem weitere Kategorien beispielsweise für Verstorbene, Neugeborene oder Personen in Quarantäne aufgenommen werden. Ziel ist es, Regeln abzuleiten, nach denen sich die Epidemie entwickelt, das heißt die Bedingungen, unter denen eine Person von einer Kategorie in eine andere wechselt.

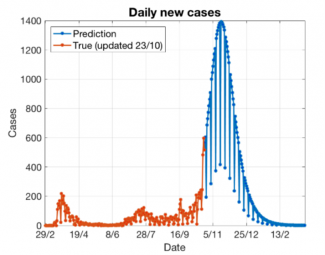
Abbildung 4 des Berichts der Task Force vom 2. November. Die blaue Kurve wurde mithilfe eines auf SIR basierenden Modells berechnet.

Schauen wir uns zunächst die Infizierten an. Vergleichbar mit dem, was wir für das exponentielle Wachstum gesehen haben, ergibt sich die Variation der Infizierten, unten mit  bezeichnet, aus den Gesunden, die sich infizieren, minus den Infizierten, die genesen. Schematisch lässt sich das Modell wie folgt darstellen:

Die Zahl der Gesunden, die sich anstecken, ergibt sich wie zuvor aus der Zahl der Kontakte  pro Zeiteinheit und der Wahrscheinlichkeit  einer Übertragung bei einem Kontakt. Weiterhin bezeichnet  die Heilungsrate. So lassen sich zu den Pfeilen Zeichen für die Zahl der Personen, die von einer Kategorie in eine andere wechseln, hinzufügen:

Das Schema lässt sich also entsprechend auch in drei Gleichungen mit den Unbekannten  und  darstellen:

S' = — np⋅SI
I' = np⋅SI — γI
R' = γI

Um die Dynamik der Epidemie im zeitlichen Verlauf zu bestimmen, muss man nun nur noch diese sogenannten Evolutionsgleichungen lösen. Grundsätzlich müsste man eine Vorlesung in fortgeschrittener Mathematik belegen, um alle Feinheiten dieser Gleichungen zu verstehen und sie lösen zu können. Heutzutage gibt es allerdings einfach zu bedienende und erschwingliche Software, die diese Arbeit für uns übernimmt.

Die Software unten ermöglicht uns die Simulation der Dynamik einer Epidemie mit einer Infektionsrate von 1 % der Bevölkerung als Ausgangspunkt. Dieser für alle Vorhersagen wesentliche Ausgangspunkt ist in der Realität allerdings schwer zu ermitteln und erfordert eine bestmögliche Vorstellung von den nicht erfassten Infizierten. Das ist der Grund für die Bedeutung großflächiger Tests und der Abwasseranalyse. Die gelbe, rote und grüne Kurve entsprechen der Entwicklung der Gesunden, Infizierten und Genesen. Mithilfe der Schieber können Sie mit den für das Modell grundlegenden Parametern experimentieren und sehen, wie sie sich beispielsweise auf die Entwicklung der Zahl der Infizierten auswirken. Es sei darauf hingewiesen, dass es genau diese Parameter sind, die wir als Bürger*innen beeinflussen können.  Barrieremaßnahmen wie das Tragen der Mund-Nasen-Bedeckung senken nämlich die Wahrscheinlichkeit einer Ansteckung bei einem Kontakt. Auch strengere Maßnahmen wie jene, die das Parlament am 29. Oktober verabschiedet hat (maximal vier Personen ohne Barrieremaßnahmen und nächtliche Ausgangssperre), werden die Zahl der Kontakte verringern.

Mit den voreingestellten Parametern kommt es bei der Kurve der Infizierten (rot) zu einem Höchststand, der eine Situation abbildet, in der sich etwa die Hälfte der Bevölkerung in einem recht kurzen Zeitabschnitt infiziert. Eine solche Situation würde unvermeidlich zu einer schweren Krise des Gesundheitssystems führen, was es unbedingt zu vermeiden gilt. Vergessen Sie also beim Spielen mit den Parametern auf keinen Fall das Motto der Epidemiologen: Flatten the curve!

Was lässt sich aus all dem schließen? Zunächst einmal, dass mathematische Modelle es uns ermöglichen, bestimmte Entwicklungen zu beziffern und Schlüsse zu ziehen. Das kann die Entscheidungsfindung erleichtern und als Begründung für bestimmte Maßnahmen dienen, wobei zu bedenken ist, dass niemand und kein Modell alle gesellschaftlichen, wirtschaftlichen und psychologischen Konsequenzen erfassen und einbinden kann. Der Blick auf eine (im schlimmsten Fall) mögliche Zukunft, den die Mathematik uns ermöglicht, erlaubt es uns aber, fundiert und angepasst zu agieren und zu reagieren, was immerhin ein guter Anfang ist.

Autor: Julien Meyer (Luxembourg Science Center)

Editoren: Christophe Ley (Professor für Mathematische Statistik am Fachbereich Angewandte Mathematik, Informatik und Statistik der Universität Gent), Michèle Weber (FNR)

Illustrationen: Wikimedia Commons, Research Luxembourg, Julien Meyer

Simulationen: Julien Meyer (erstellt mit geogebra.org auf der Grundlage der Daten/Grafiken des Berichts von Research Luxembourg)